最小步数（普及）

ireallyakioi首先发行, 现名GOD_HJ（第一次写博客，虽然很简单，但敬请斧正）

一般算法： BFS)

因为DFS回溯太满了，所以用BFS。 （思路度娘一搜就有，不在过多解释解释）。

code:

#include <bits/stdc++.h>
using namespace std;
int a[105][105];
int dx[]={-2,-2,-2,-2,-1,1,2,2,2,2,1,-1};
int dy[]={-2,-1,1,2,2,2,2,1,-1,-2,-2,-2};
int main(){
    for(int i=0;i<100;i++)
        for(int j=0;j<100;j++) 
            a[i][j]=-1;
    a[0][0]=0;
    int x1,y1,x2,y2;
    scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
    queue<int> x,y,bs;
    x.push(0);
    y.push(0);
    bs.push(0);
    while(!(x.empty()&&y.empty())){
        for(int i=0;i<12;i++){
            int xx=x.front(),xy=y.front(),bss=bs.front()+1;
               xx+=dx[i];
            xy+=dy[i];
            if(xx<0||xx>99||xy<0||xy>99) continue;
            if(a[xx][xy]==-1){
            }
        }
        x.pop();
        y.pop();
        bs.pop();
    }
    printf("%d\n%d",a[x1-1][y1-1],a[x2-1][y2-1]);
}

O(1)算法：算数（朴实无华）

这里只讨论第一次输入，第二次同第一次。

设输入为$x,y$,则$(1,1) (1,y) (x,y) (x,1)$为一个矩形（矩形的长，宽是长度（坐标-1），不是坐标）。

那么，$最小步数=ceil(长~~（长的一条边是长）~~÷2)$,理由如下：

为了方便描述，把所有长方形“立起来”。

如果比较巧：（如图）。

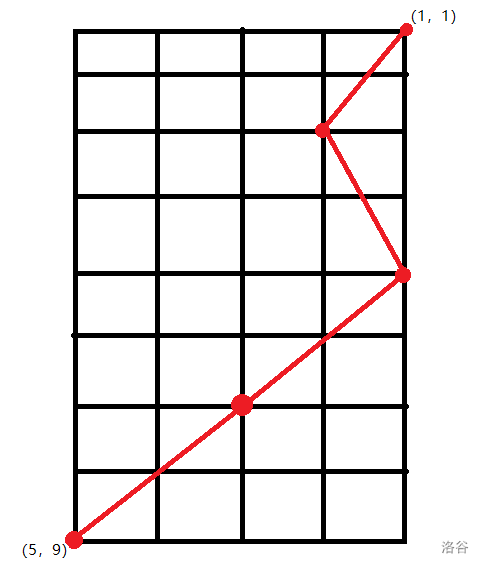
那么就可以一直以田字跳，直到到达了边界，在“左右左右”跳；

所以 $最小步数=长÷2$。

那如果不巧：（如图）。

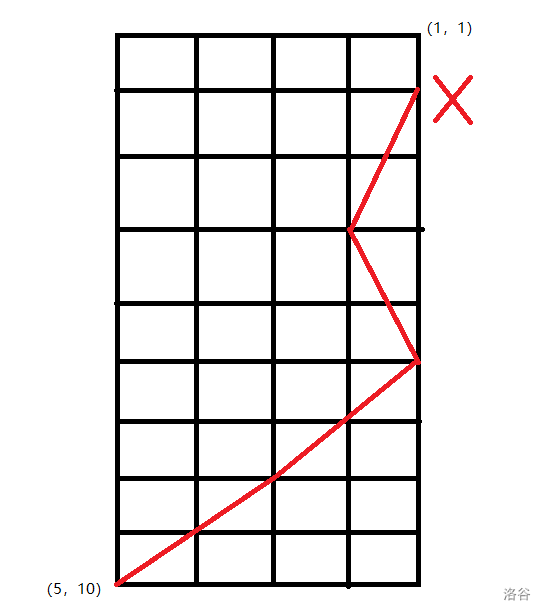
那么就在开始时先向有一下，在跳田字，“左右左右”……（如图）。

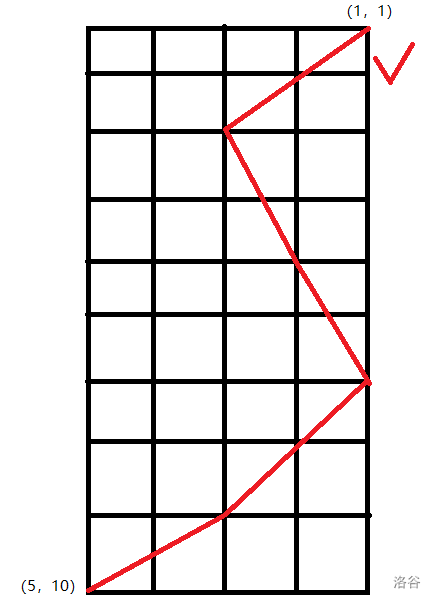
这个图同时也证明了，当长不整除4时的画法。

此时， $最小步数=ceil(长÷2)$。

如果宽是奇数，那就先走一个“日”在走“田”（相当于把奇数减一化成偶数），不会影响结果（感谢pink_rabbit提醒）。

但是！！

可以发现，当 $长 \le 2$ 时，方法并不适用，所以，需要特判。

code 见下（建议自我思索一下）……

·

·

·

·

·

·

code

#include<bits/stdc++.h> 
using namespace std;
int main(){
    for(int i=0;i<2;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        int wlong = max(x-1,y-1);//长
        if(wlong<=1){//特判
            if(x==2&&y==2) printf("%d\n",3);
            else printf("%d\n",2);
            continue;
        }else if(wlong==2){
            printf("%d\n",1);
            continue;
        }
        printf("%d\n",int(wlong/2.0+0.5));//输出
    }
}

吊打集训队不是我说的。